Pulse-code modulation (PCM) is a method used to digitally represent sampled analog signals. It is the standard form of digital audio in computers, Compact Discs, digital telephony and other digital audio applications. In a PCM stream, the amplitude of the analog signal is sampled regularly at uniform intervals, and each sample is quantized to the nearest value within a range of digital steps.
Linear pulse-code modulation (LPCM) is a specific type of PCM where the quantization levels are linearly uniform.^[5] This is in contrast to PCM encodings where quantization levels vary as a function of amplitude (as with the A-law algorithm or the μ-law algorithm). Though PCM is a more general term, it is often used to describe data encoded as LPCM.
A PCM stream has two basic properties that determine the stream's fidelity to the original analog signal: the sampling rate, which is the number of times per second that samples are taken; and the bit depth, which determines the number of possible digital values that can be used to represent each sample.

Modulation

Sampling and quantization of a signal (red) for 4-bit PCM

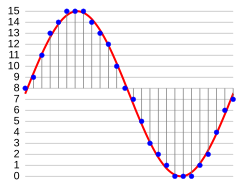
In the diagram, a sine wave (red curve) is sampled and quantized for PCM. The sine wave is sampled at regular intervals, shown as vertical lines. For each sample, one of the available values (on the y-axis) is chosen by some algorithm. This produces a fully discrete representation of the input signal (blue points) that can be easily encoded as digital data for storage or manipulation. For the sine wave example at right, we can verify that the quantized values at the sampling moments are 8, 9, 11, 13, 14, 15, 15, 15, 14, etc. Encoding these values as binary numbers would result in the following set of nibbles: 1000 (2³×1+2²×0+2¹×0+2⁰×0=8+0+0+0=8), 1001, 1011, 1101, 1110, 1111, 1111, 1111, 1110, etc. These digital values could then be further processed or analyzed by a digital signal processor. Several PCM streams could also be multiplexed into a larger aggregate data stream, generally for transmission of multiple streams over a single physical link. One technique is called time-division multiplexing (TDM) and is widely used, notably in the modern public telephone system.
The PCM process is commonly implemented on a single integrated circuit generally referred to as an analog-to-digital converter (ADC).

Demodulation

To recover the original signal from the sampled data, a "demodulator" can apply the procedure of modulation in reverse. After each sampling period, the demodulator reads the next value and shifts the output signal to the new value. As a result of these transitions, the signal has a significant amount of high-frequency energy caused by aliasing. To remove these undesirable frequencies and leave the original signal, the demodulator passes the signal through analog filters that suppress energy outside the expected frequency range (greater than the Nyquist frequency ).^{[note 1]} The sampling theorem shows PCM devices can operate without introducing distortions within their designed frequency bands if they provide a sampling frequency twice that of the input signal. For example, in telephony, the usable voice frequency band ranges from approximately 300 Hz to 3400 Hz. Therefore, per the Nyquist–Shannon sampling theorem, the sampling frequency (8 kHz) must be at least twice the voice frequency (4 kHz) for effective reconstruction of the voice signal.
The electronics involved in producing an accurate analog signal from the discrete data are similar to those used for generating the digital signal. These devices are Digital-to-analog converters (DACs). They produce a voltage or current (depending on type) that represents the value presented on their digital inputs. This output would then generally be filtered and amplified for use.

Weapons Sensor Technology Detects Rotten Meat, Ripe Fruit

A John D. MacArthur Professor of Chemistry at MIT, Timothy Manning Swager has created tiny sensors that detect chemical weapons and explosives but he also sees the potential for the technology to be used in a civilian application:

Professor Swager who described Chemosensors as molecule-based devices designed and synthesized to detect a specific chemical signal directed the use of the chemosensory research to harness unique properties of conjugated organic polymers (molecular wires). The research group has demonstrated some years ago that “wiring molecular recognition sites in series” leads to ultra-high sensitivity and that this approach has universal applicability for the amplification of chemosensory responses. The principles developed by their group can amplify chemosensory signals by many orders of magnitude. Their sensor principles are now broadly practiced by many research groups around the world and are the basis of a number or emerging sensor technologies.

With funding from the US Army, Professor Swager, has altered the chemistry in the sensors so that they can detect rotting meat and fruit ripeness. “What I would really like to make is a sensor that can be used in a grocery store to tell if a tomato tastes good,” he says. As part of smart packaging, the business card-sized sensors can be embedded in meat crates being shipped to a grocer. Upon arrival, a worker can scan the shipment with the press of a button to get an instant readout of which crates have questionable contents. “It’s a lot like a passive transponder in your car, which can be powered and read when you drive through the tollbooth,” says Swager.

The sensors’ smarts come from Swager’s combined use of carbon nanotube-based circuitry and radio frequency identification (RFID) tagging technology. When the sensor receives a pulse of power from a remote scanner, electricity flows through the carbon-nanotube circuits. If the target chemical is present, it will either enhance or slow the electron flow and cause a measurable change in electrical resistance. That signal plus the sensor’s RFID tag allow the grocer to quickly locate and cull bad pieces of meat.

Swager sees a range of other potential applications, such as installing fruit ripeness sensors in greenhouses to allow farmers to precisely time harvests and embedding sensors that detect explosives and other harmful agents in public transportation passcards to improve public safety.

Source